Hey Everyone👋👋
Graphs are really an important part of our though we may not be aware of them. There are n number applications of Graph as we can visualise any data in a graph format.
Eg :
- LinkedIn Connections (Social Graph)
- Navigation Systems
- Recommendation Systems and much more...
In this blog, we will see how depth-first search works. Now the depth-first search is a graph traversal algorithm meaning it is an algorithm to go through the graph and do processing as and when required.
Now without any further statements, let's dive in...

🌟Let's get Started
Let us first understand what a graph is and what does looks like?
A graph is a non-linear data structure consisting of Vertices and Edges. Woosh! This is a very formal definition 🥵.
In simple terms, a graph is a set of some variables which we call vertices here and some relationships which call as edges. Here is what it looks like :
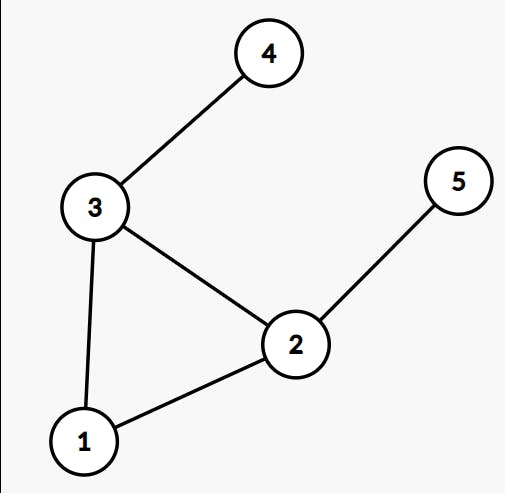
Here 1, 2, 3, 4, 5 are nodes and connections between them are called edges. Enough of the Graph explanation, let us look at DFS now. 🤚
📉 Depth First Search - DFS
As I mentioned earlier DFS is a graph traversal algorithm meaning that it helps us go through graphs. There is also another graph traversal algorithm known as Breadth-First Search (BFS). The goal of both algorithms is the same but the methods to do that are different.
Let us take a look at the working of DFS :
Step 1: Start with any node 'N'
Step 2: Mark 'N' as Visited
Step 3: Explore all the Nodes connected to 'N'
Step 4: While Exploring any node mark the specific node as Visited
Step 5: If a node is visited already do not explore it again
Step 6: Stop when all the nodes are visited
Sounds easy, does it ?
It might not but it is way too easy, you'll have a clear understanding of it once we go through an example.
Let us take the Graph mentioned above :
2 ---- 4
/ |
1 |
\ |
3 ---- 5
1. We can start with any node, let us say we start with 2
2. After visiting 2, first explore all nodes which are connected to node 2
3. As node 1 is not explored go to node 1 (you can also go to node 3 or 5)
4. Now first explore all nodes connected to node 1
5. As node 3 is not explored goto node 3
6. Now explore all nodes connected to node 3
7. Here we can choose 2 or 5, but as 2 is already visited we will choose 5
8. As node 5 is a leaf node, we now go back to exploring node 1
9. Here we visited nodes 2 and 3 already, so we go back to node 2
10. Atlast at node 2 we are left with node 4 as nodes 1 & 3 are explored
So in this way, we have visited and explored the whole graph --> 2,1,3,5,4
The reason we mark nodes as "visited" is that , in the graph there are cycles due to which we might end up in an endless loop of visiting them, so once we visit a node, in order to avoid revisiting it again we mark it as visited.
⌛Time Complexity Analysis

If we say that the graph has 'v' number of nodes and 'e' number of Edges. Then the time complexity of DFS is in Order of \(v+e\) that is it can be represented in the form :
$$ O( v + e ) $$
The space complexity of the algorithm is \(O(v)\).
👨💻Code

In this code below, the adjlist is an adjacency list.
Now an adjacency list is a representation of a graph in which each node has a list of nodes that are adjacent to it that is the nodes that are connected to it.
Here is a recursive approach that builds a stack due to recursion.
#include<bits/stdc++.h>
using namespace std;
unordered_map<int,bool> visited;
unordered_map<int,vector<int>> adjlist;
void dfs(int node){
visited[node] = true; // Mark the node visited
cout << node << " "; // Print the node
// loop through adjacent nodes
for (int i=0 ; i < adjlist[node].size() ; i++) {
if( visited[ adjlist[node][i] ] == false )
dfs(adjlist[node][i]); // explore the node if not visited
}
}
int main(){
vector<pair<int,int>> relationships = {
{1,2},
{1,3},
{2,3},
{2,4},
{3,5}
};
// build Adjacency list
for(auto x : relationships){
adjlist[x.first].push_back(x.second);
adjlist[x.second].push_back(x.first);
}
dfs(2);
return 0;
}
Output :
2 1 3 5 4
You can play with it here.
Here is another approach explicitly using stack. This is indeed a good application of stack .
Psuedo Code for stack approach :
1. Select a start node
2. Push the node to stack
3. do steps 4 and 5 until the stack is not empty
4. Pop a value from stack say 'N'
5. If node 'N' is not visited do steps 6 and 7 else goto step 4 again
6. Mark 'N' as Visited
7. do step 8 for all adjacent nodes to 'N'
8. Push adjacent node 'x' if x is not visited.
9. End when stack is empty
Code with Stack in action
#include<bits/stdc++.h>
using namespace std;
unordered_map<int,bool> visited;
unordered_map<int,vector<int>> adjlist;
void dfs(int node){
stack<int> s;
s.push(node); // push source node
while(!s.empty()){ // loop until stack is empty
int n = s.top(); // get top element
s.pop(); // pop from stack
if(visited[n]==false){
visited[n] = true; // mark visited;
cout<<n<<" ";
// loop through adjacent nodes
for (int i=0 ; i < adjlist[n].size() ; i++) {
if( visited[ adjlist[n][i] ] == false )
s.push(adjlist[n][i]); // push to stack if not visited
}
}
}
}
int main(){
vector<pair<int,int>> relationships = {
{1,2},
{1,3},
{2,3},
{2,4},
{3,5}
};
for(auto x : relationships){
adjlist[x.first].push_back(x.second);
adjlist[x.second].push_back(x.first);
}
dfs(2);
return 0;
}
Output :
2 4 3 5 1
You can play with code here.
Note that you can start with any node in DFS.
🎯Final Thoughts
Amazing! Congrats on making it to the end of the article!
DFS is a great way to enter into the graphs world. Do try to implement the code on your own, you will get a much better understanding by doing that.
Here is a good question if you want to get a hang of it.
Thanks for reading the article. I hope you liked it. ✌️✌️ Give me a follow if you liked it and do comment! I am open to discussion.🎉🎉
Cheers! 🥂


